In many evolutionary optimization applications, the evaluations are noisy and uncertain. With a large population, it is therefore likely that the candidates that seem to be the best simply got lucky during evaluation—and their future performance is going to be disappointing. Yet experience with evolutionary optimization suggests that the evaluations and winner selections are more reliable than they should be. How can that be?
Indeed if each evaluation was independent from the other, such multiple hypotheses could be a problem. However, the evaluations are not independent. Each candidate is composed of components that have been tested many times before—as part of ancestor candidates. Candidates later in evolution inherit confidence from all those earlier test. Can this phenomenon be quantified?
Indeed it can. A Gaussian Process (GP) can be built based on all the solutions collected during the evolution. The fitnesses of nearby solutions in the search space are correlated, and the GP captures this correlation. It can then be used to predict the mean and variance of the fitness of a new solution nearby. The more similar solutions are explored, the narrower the confidence intervals around them become!
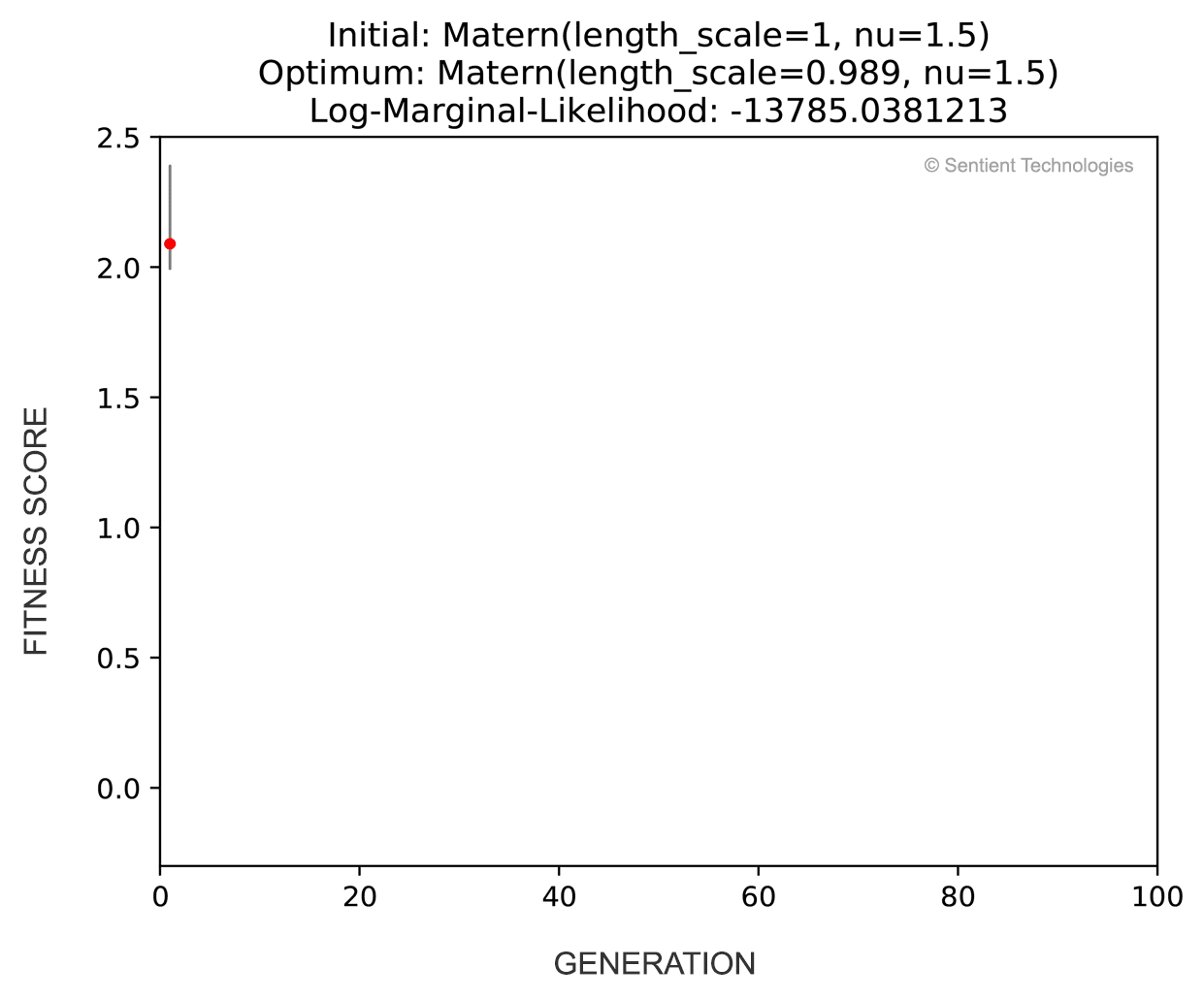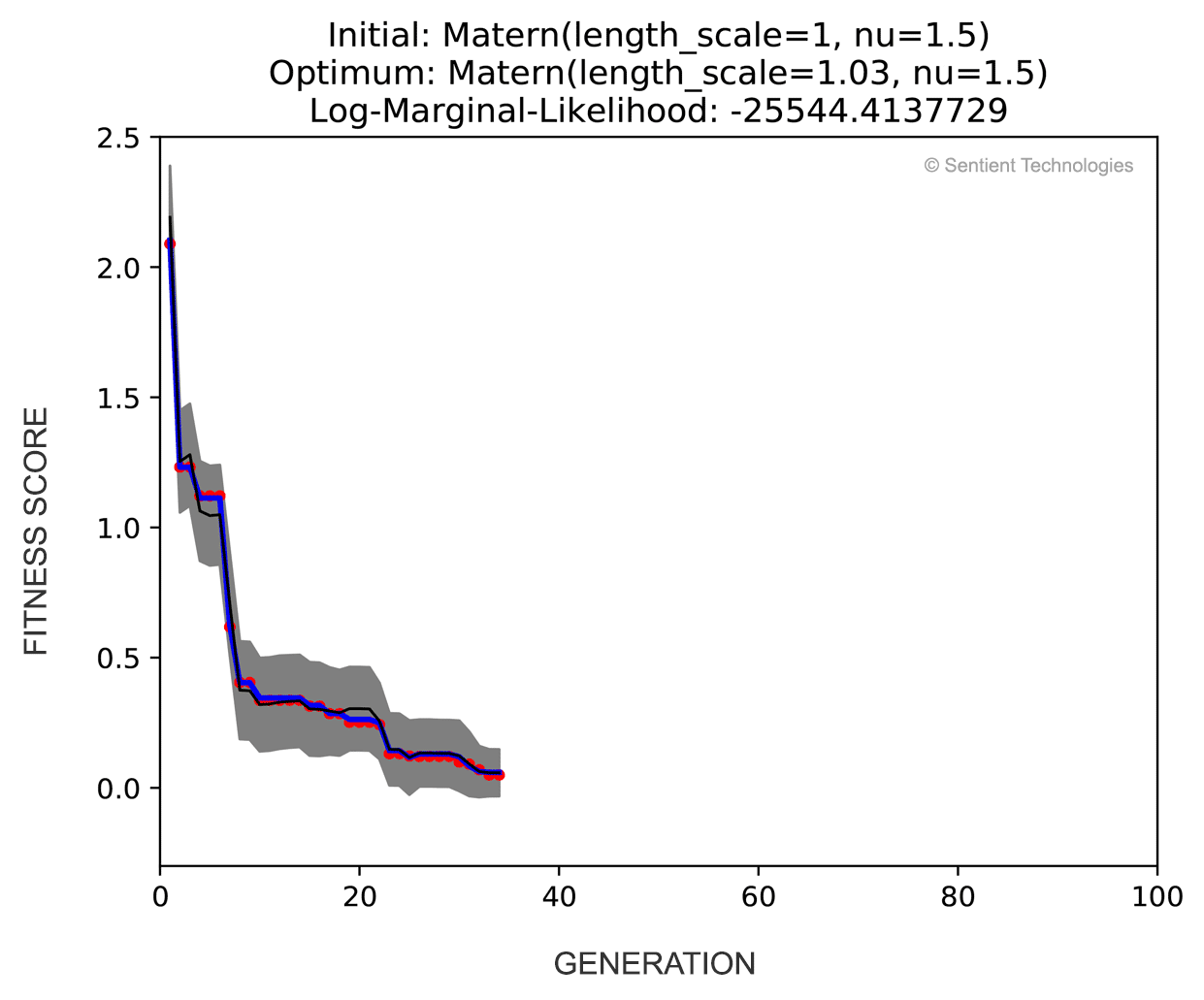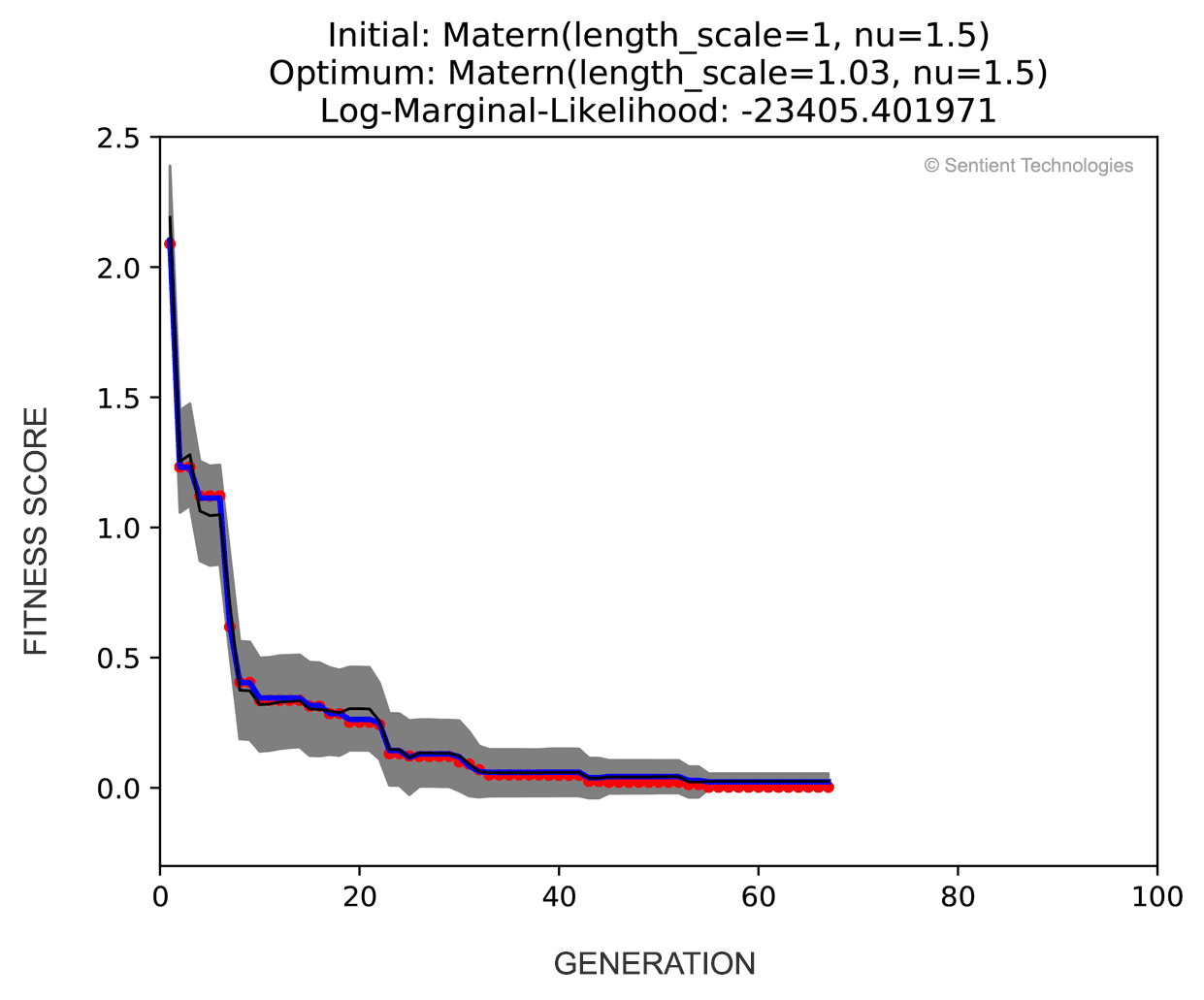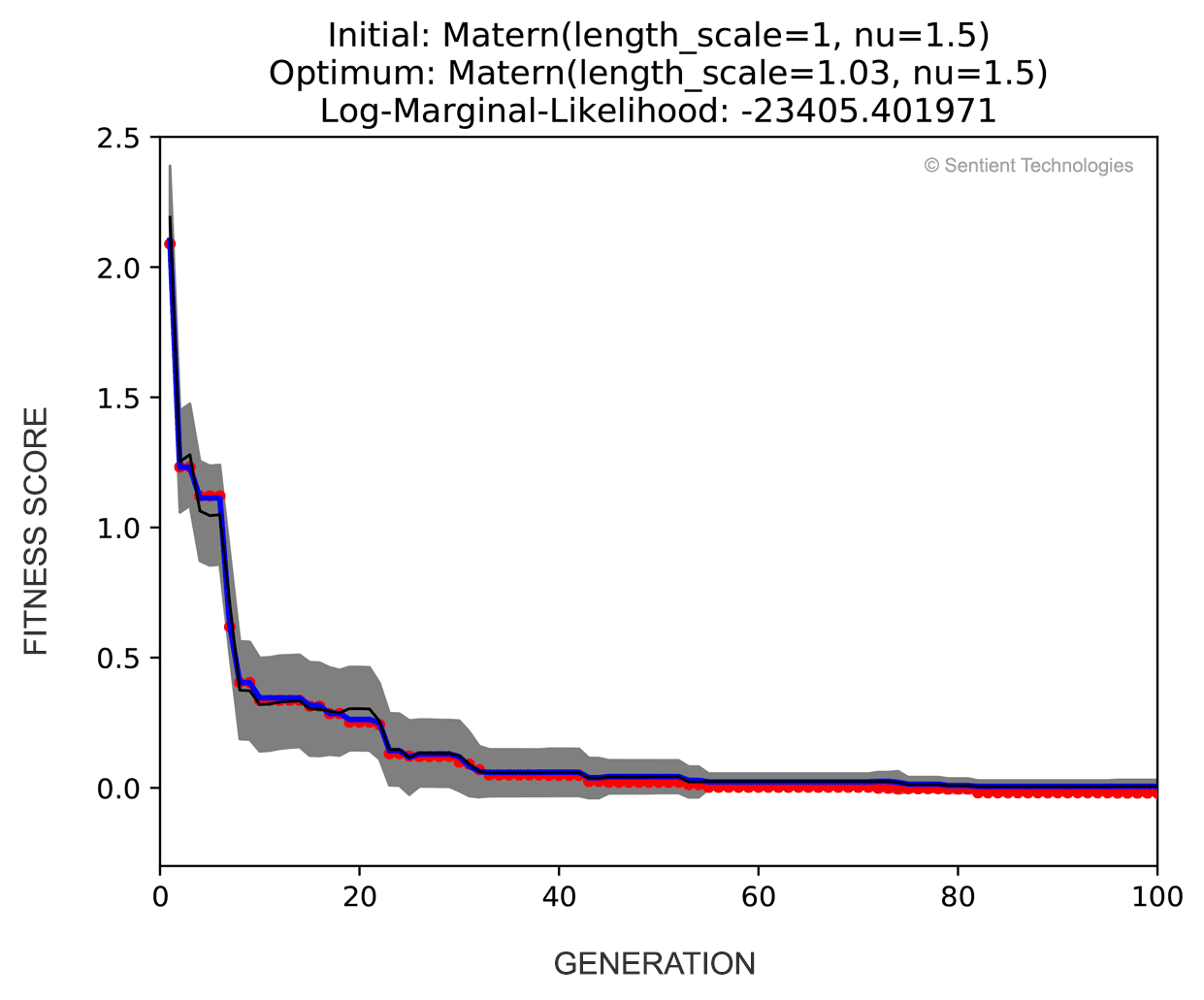
The demo above shows the performance of differential evolution on a numerical optimization problem. A Gaussian Process with hyperparameter-optimized Matern kernel was used to calculate the 95% confidence interval (gray area) for the best-obtained solution (red dot) in each generation. The fitness values used for modeling come from a noisy observation. The black curve and blue curve represent the estimated mean for fitness distribution and true fitness without noise, respectively. In this case, both the estimation accuracy and the confidence of the best solution are increasing, indicating that more and more confidence is inherited from past generations. This observation explains quantitatively why Evolutionary Algorithms result in more reliable results in uncertain domains than simple statistical considerations would suggest.