This demo shows how the composite novelty method of Paper 1 makes it possible to find solutions even in highly deceptive search spaces. The problem of finding a minimal 8-line sorting network is used as the example. The composite novelty method is compared to NSGA-II, i.e. a standard multi-objective optimization method, in two ways: the spread of the population in the multiobjective space, and the spread of the population in the behavioral space. The illustrations show that (1) whereas NSGA-II population spans a wide range of tradeoffs, composite novelty is focused on a narrower range of more useful tradeoffs; and (2) whereas NSGA-II population focuses on a limited, clustered set of behaviors, composite novelty population spans a wide range of behaviors.
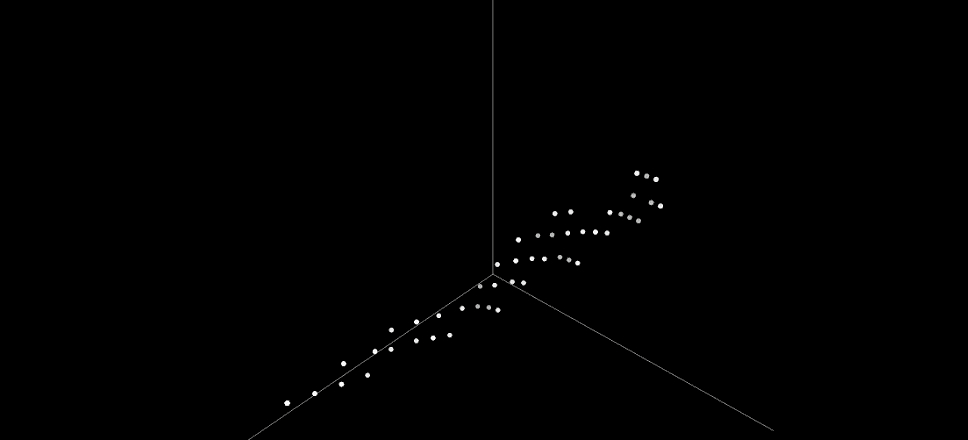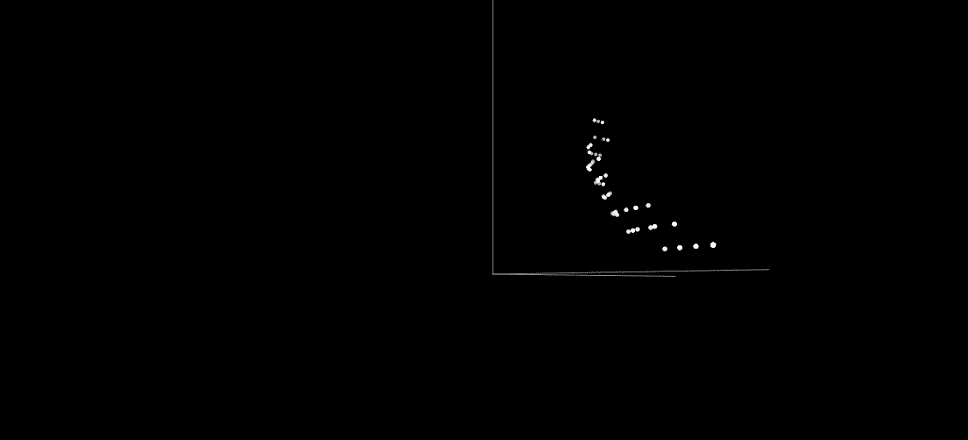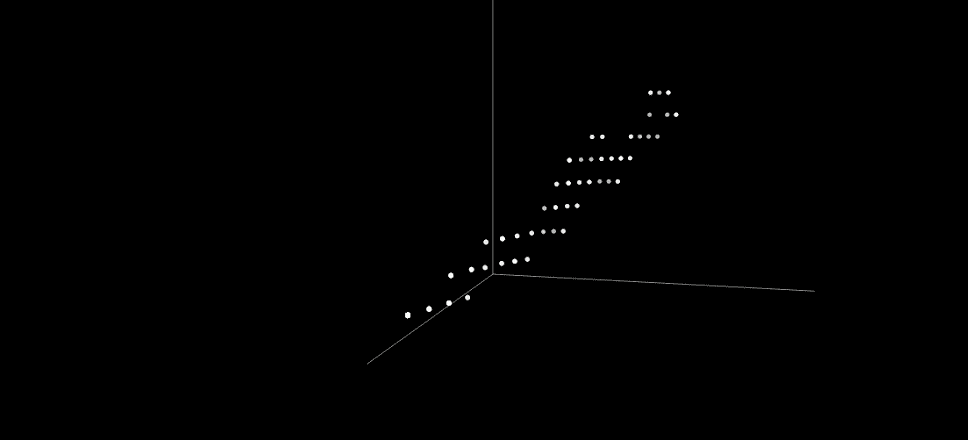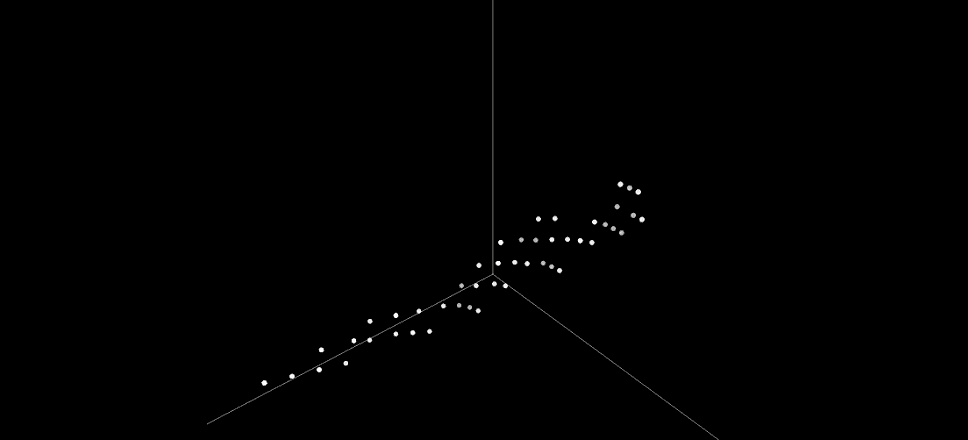
This illustration above shows the candidates belonging to the first few layers of the NSGA-II Pareto front in the multiobjective space of the three objectives: correctness, the number of layers in the network, and the number of comparators in the network. The animation rotates the display so that it is easier to see the distribution of candidates in this space. At this point, the optimization process was stuck with the best network that sorted correctly, but had a suboptimal size of 8 layers and 22 comparators. The Pareto front spans a wide area, but also includes solutions that represent extreme tradeoffs such as a network with a single layer, or a single comparator, that are not useful in the search of better solutions. Can we do better?

The above illustration shows the corresponding candidates in the same space and at the same stage of optimization for the composite novelty method. Because the objectives used for the optimization are composite of the original objectives, the candidates now span a narrower area in the original objective space, in particular focusing in the central area where the most useful trade-offs are. At first glance it seems that the method has lost diversity—yet it can proceed from here to find better solutions (unlike NSGA-II). Why does it not get stuck? Let’s take a look at the behavior space for a clue.

The behavior in this example is characterized by the number of times a value in each line is swapped across all possible binary inputs. For visualization, this 8D space is then projected to 3D. The illustration above shows the same NSGA-II candidates in the behavioral space. Even though these candidates were diverse in the multiobjective space, they are much less so in the behavioral space: They form two dense clusters, and do not cover much of the different behaviors. The reason is the selection in NSGA-II is based solely on objective diversity, not behavioral diversity. Such a lack of diversity is the reason why evolution gets stuck on suboptimal solutions.
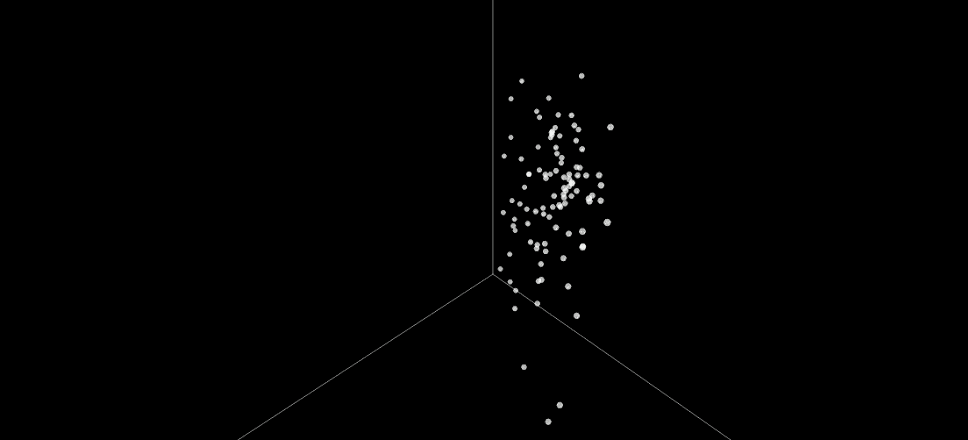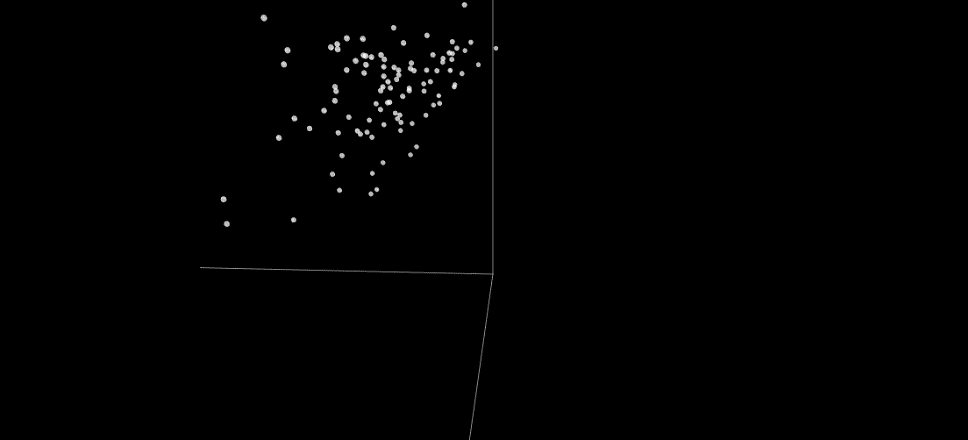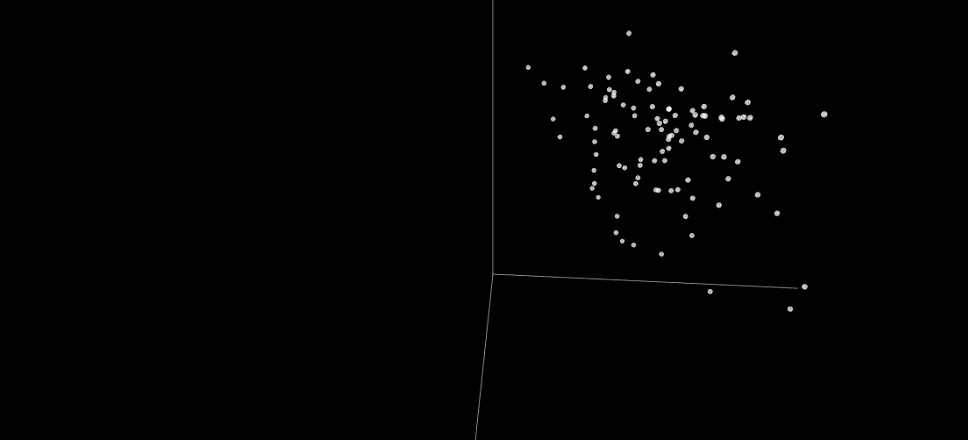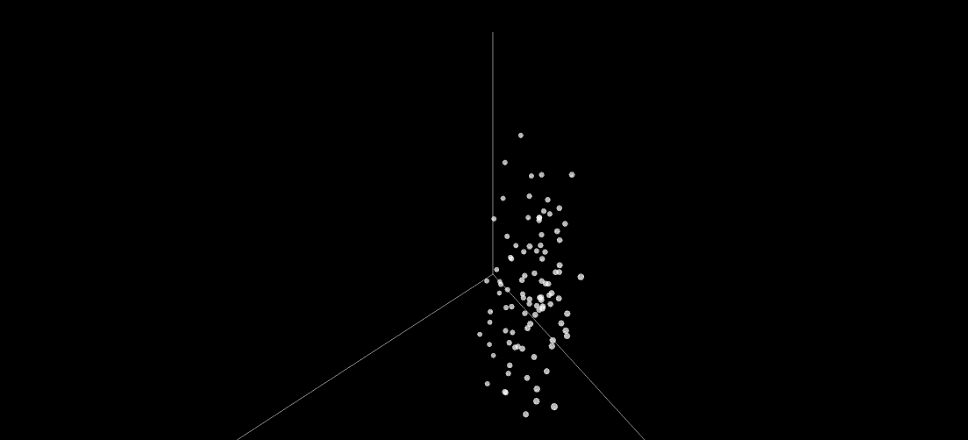
In contrast, Composite Novelty uses an explicit measure of novelty to decide which candidates to discard and which to keep during selection. As a result, the candidate behaviors span a wider range and more evenly than those of NSGA-II. This diversity makes it possible for the method to proceed where NSGA-II gets stuck: it can make drastic changes to the solutions to minimize them further, and it will eventually find the optimal solution of 6 layers and 11 comparators.
In this manner, Composite Novelty provides a promising solution to the third aspect of hard problems, i.e. those where the search space is deceptive. It can also be useful for problems where the goal is to discover a diverse set of good solutions, as is the case in many multiobjective problems.